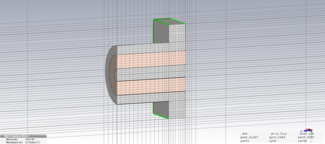
Part of my work at the Cavendish Laboratory involves optimisation of the SKA Low aperture array antenna. As a result, a substantial amount of FEKO gets used. During my efforts, I created a script that allows for parameter sweeps over a parameterised FEKO model over an arbitrary number of input dimensions. Using a Lua scripting built into CADFEKO, it is possible to generate geometries where structures can be added and removed. This comes in handy when you want to change the number of elements in your Yagi or LPDA antenna. I found this script extremely useful in optimising my antenna design and hope it can be of use to the larger FEKO community.
Usage:
The current script has 3 files:
- Model.lua
- parametersweep.lua
- Parametric_Model_Source.cfx
Model.lua is your own antenna scripting file (add antenna here). I found the FEKO documentation (F1) very useful for finding functions that I needed. Use this file as an example to create your own antenna.
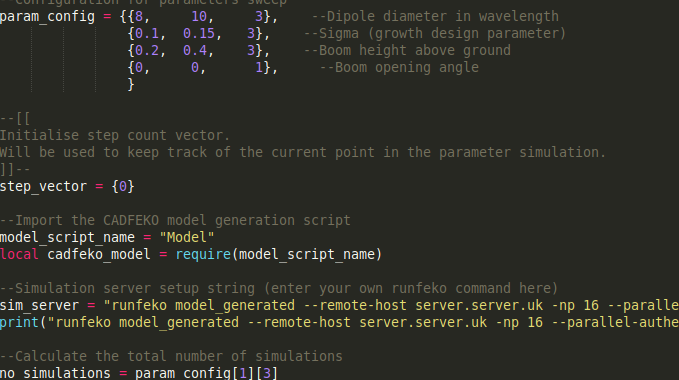
parametersweep.lua handles the loop process that generates the CADFEKO geometry from Model.lua and invokes runfeko to simulate the file. You might need to create a results folder on your machine for the script to copy the results into. During some experimentation, I also found it useful to call python scripts from the main loop to calculate metrics from the results.
Parameteric_Model_Source.cfx exists because I was too lazy to figure out how to add wire ports and voltage sources to the parametric antenna model. Nevertheless, this file is used to define your result requests and other simulation parameters like frequency, etc.
To start the script, open CADFEKO by opening the Parametric_Model_Source.cfx. Open the scripts editor from the ribbon bar. You need to careful here not to edit or use old scripts, FEKO reopens the last scripts that were used. For safety, I tend to close all the tabs and make sure I open the correct script. Finally with the parametersweep.lua file open, click the run command and get ready for some chaos on the screen.
If you have some improvements that you have added to your own script, let me know so that I can add it to this page. In its current state, it does not work on Linux or Mac. Also, during simulation, it will occasionally grab your mouse focus when it opens and closes the cmd window.
Download the script here
Remember, antennas should roam free. No antenna deserves to be caged and crammed into your smartwatch.
Example of an antenna in the wild (SKALA2 https://www.icrar.org/)